Suele decirse que a Newton se le ocurrió la Ley de la Gravitación Universal cuando le cayó una manzana en la cabeza. Ya sea esto cierto o no, él pensó que “algo” atraía la manzana y a todos los objetos en la Tierra hacia abajo y le llamó fuerza de gravedad. Dado que es necesaria una fuerza para mantener un objeto girando en círculos dedujo que esta fuerza era la gravedad. Después de muchos cálculos, llegó a la fórmula siguiente:
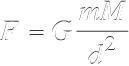
donde G es la constante de la gravitación universal con un valor de
6.67 × 10−11 Nm2/ kg2; m y M son las masas de los cuerpos en cuestión y d es la distancia que separa a estos cuerpos.
Cuando estamos en la Tierra,
M = 5.976 x 10 24 kg y d es el radio de la Tierra que vale aproximadamente: R = 6.378 × 10 6 m. Si suponemos que tu masa es de 60 kg, entonces tu peso será:
F = 587.92 N
Si se calcula de la manera usual: F = mg, es decir. F = (60 kg)(9.8052 m/s2) = 588.312.
Se obtiene prácticamente el mismo resultado, la diferencia entre ambos es 0.391.
Una ecuación muestra la relación entre las variables. Si tienes un ojo experto, tal vez visualices cómo influyen los valores de la masa y de la distancia en la fuerza de gravedad, pero quizá para la mayoría es necesario ver paso a paso a paso de qué manera se modifica. Lo anterior significa suponer varios valores de las variables independientes y hacer muchas operaciones para observar el comportamiento.
¿Te imaginas cuánto tiempo te tomaría? Por fortuna, en la actualidad existen las hojas de cálculos que nos permiten hacer la tarea anterior en segundos en lugar de horas.
Primero analizaremos cómo influye la variable M1 a la fuerza de gravedad. Es importante que cuando se hace este tipo de análisis, solo se modifique el valor de una variable y se fije con un valor constante todas las demás. Es este caso, se mantendrá constante M2 y d, se les fijará un valor arbitrario de 1 kg y 1 m respectivamente.
